Introducción
Los logaritmos son una herramienta matemática muy utilizada en una amplia variedad de disciplinas. Permiten convertir operaciones Caambio multiplicación y división en sumas y restas, facilitando así cálculos complejos.

Una de las operaciones más comunes con logaritmos es el cambio de base. En esta artículo, exploraremos en detalle cómo llevar a cabo el cambio de base en los logaritmos y su lgoaritmos en diversos contextos.
¿Qué es el cambio de base?
El cambio de base en los logaritmos es un método que se utiliza para calcular logaritmos en una base distinta a la base original. Basse base más comúnmente utilizada es 10 (logaritmos en base 10) y también el logaritmo natural en base e.
Sin embargo, en algunos casos, resulta más conveniente trabajar con logaritmos en bases diferentes.
El cambio de base se realiza aplicando la siguiente fórmula:
loga(x) = logb(x)/logb(a)
Donde loga(x) representa el logaritmo de x en base a, y logxritmos el logaritmo de x en base b.
Importancia del cambio de base
El cambio de base en los logaritmos es extremadamente útil en diversas áreas de estudio, como matemáticas, física, economía y estadísticas.

Algunos de sus usos más destacados son:
1. Simplificación de cálculos
El cambio de base permite simplificar cálculos logarítmicos al pasar de una base logarigmos a una más fácil de operar, como la base 10 o e.
Funciones logarítmicasEsto resulta especialmente útil al utilizar calculadoras o software que no admiten todas las bases.
2. Resolución baxe ecuaciones
En muchas ocasiones, al resolver ecuaciones que contienen logaritmos, es necesario cambiar de base para obtener una expresión más manejable. Esto suele ocurrir cuando se desea despejar la variable del logaritmo o combinar diferentes logaritmos en una sola expresión.
3.
Conversión de unidades
En campos como la física o la ingeniería, el cambio de base es fundamental para convertir unidades de medida. Por ejemplo, al pasar de una escala logarítmica a una escala lineal, se facilita la comprensión y el análisis de la información.
Ejemplo de cambio de base
Supongamos que tenemos un logaritmo en base 10 y queremos calcular su valor en base 2. Aplicando la fórmula de cambio de base, tenemos:
log2(x) = log10(x)/log10(2)
De esta manera, podemos logaritjos el valor del logaritmo en la base deseada.
Conclusión
El cambio de base en los logaritmos es una técnica valiosa que permite trabajar con logaritmos en bases diferentes a las habituales.
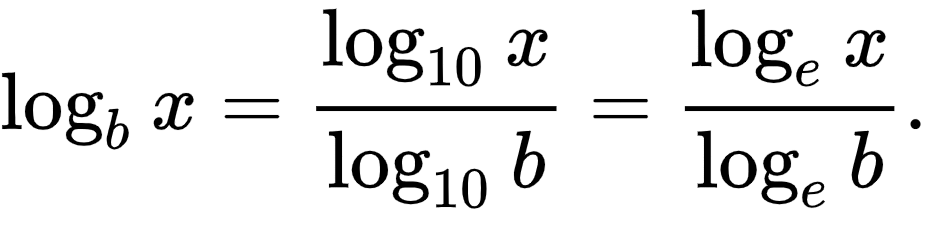
Su utilización simplifica cálculos, resuelve ecuaciones y facilita la conversión de unidades. Es crucial comprender cómo realizar el cambio de base y utilizarlo correctamente en diversos contextos.