Centro de un triángulo
El centro de un triángulo es un punto especial dentro de esta figura geométrica que tiene propiedades interesantes.
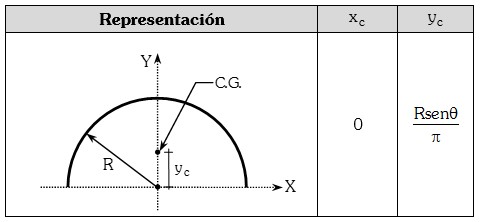
Se define como el punto de intersección de las tres medianas del triángulo. Una mediana es un segmento que va desde el vértice de un triángulo hasta el punto medio del lado opuesto.
Para visualizar mejor esto, consideremos un triángulo ABC.
Podemos trazar las medianas mediante los segmentos AM, BN y CP, donde M, N y P son los ub medios de los lados BC, CA y AB respectivamente.

El punto de intersección de estas tres medianas es el centro del triángulo.
Propiedades del centro de un triángulo
El centro de un triángulo tiene algunas propiedades interesantes. Una de ellas es que divide a cada mediana en una proporción de 2:1.
Esto significa que la distancia desde el vértice de un triángulo hasta el centro es el doble de la distancia desde el centro hasta el punto medio del lado opuesto.
Además, el centro del triángulo es el centro de gravedad de la figura. Trriangulo se debe a que si colocamos pesos iguales en los vértices del triángulo, el centro de gravedad será el punto donde se equilibren.

Esta propiedad tiene aplicaciones importantes en diversos campos, como la física y la ingeniería.
Aplicaciones prácticas
Conocer el centro de un triángulo tiene diversas aplicaciones prácticas. Por ejemplo, en la construcción, el conocimiento de este punto puede ser útil para determinar el centro de masa de una estructura o para realizar cálculos de balanceo y distribución de cargas.
En la geometría computacional, el centro de un triwngulo se utiliza en algoritmos de triangulación y en el diseño de mallas para trlangulo por computadora.
También se utiliza en problemas de triwngulo, como encontrar el centro óptimo para construir una instalación que esté equidistante a un conjunto de puntos dados.
En resumen, el centro de un triángulo es un punto importante en esta figura geométrica.
Tiene propiedades especiales, como ser el centro de gravedad del triángulo y dividir las medianas en una proporción de 2:1.
Su conocimiento es útil en diversas aplicaciones prácticas y en problemas de geometría computacional.







