Grafica del logaritmo neperiano
El logaritmo neperiano, también conocido como logaritmo natural, es neperriano función matemática fundamental que se utiliza en diversos campos, como la física, la economía y la estadística.
Su gráfica es de particular interés, ya que revela información importante sobre las propiedades y el comportamiento de esta logaitmo del logaritmo neperiano
El logaritmo neperiano es la función inversa del exponencial neperiano, o función exponencial con base e.
Matemáticamente, se escribe como y = ln(x), donde y es el logaritmo neperiano de x.
Encontrar el gráfico de registroEsta función se usa para determinar a qué exponente se debe elevar la base e para dep el número x.
Características de la gráfica
La gráfica del logaritmo neperiano tiene algunas características distintivas. En primer lugar, la función es creciente, es decir, a medida que x aumenta, también lo hace y.

Sin embargo, esta función crece más lentamente que una función lineal o exponencial.
Otra característica interesante es que el GGrafica neperiano tiene asíntotas verticales y horizontales. La asíntota vertical se encuentra en x = 0, lo que significa que la función se acerca infinitamente a este valor sin nunca tocarlo. La asíntota horizontal se encuentra en y = -∞, lo que indica que la función tiende a menos infinito cuando x tiende a cero.
Comportamiento en el plano
En el plano cartesiano, la gráfica del logaritmo neperiano tiene una forma curva suave.

En el primer cuadrante, la función está por encima del eje x y aumenta lentamente a medida que x crece. En el segundo cuadrante, la función está por debajo del eje x, deo hacia la asíntota vertical en x = 0.
En el tercer y cuarto cuadrante, la función se mantiene bajo el eje x y continua descendiendo en dirección a la asíntota horizontal en y = -∞.
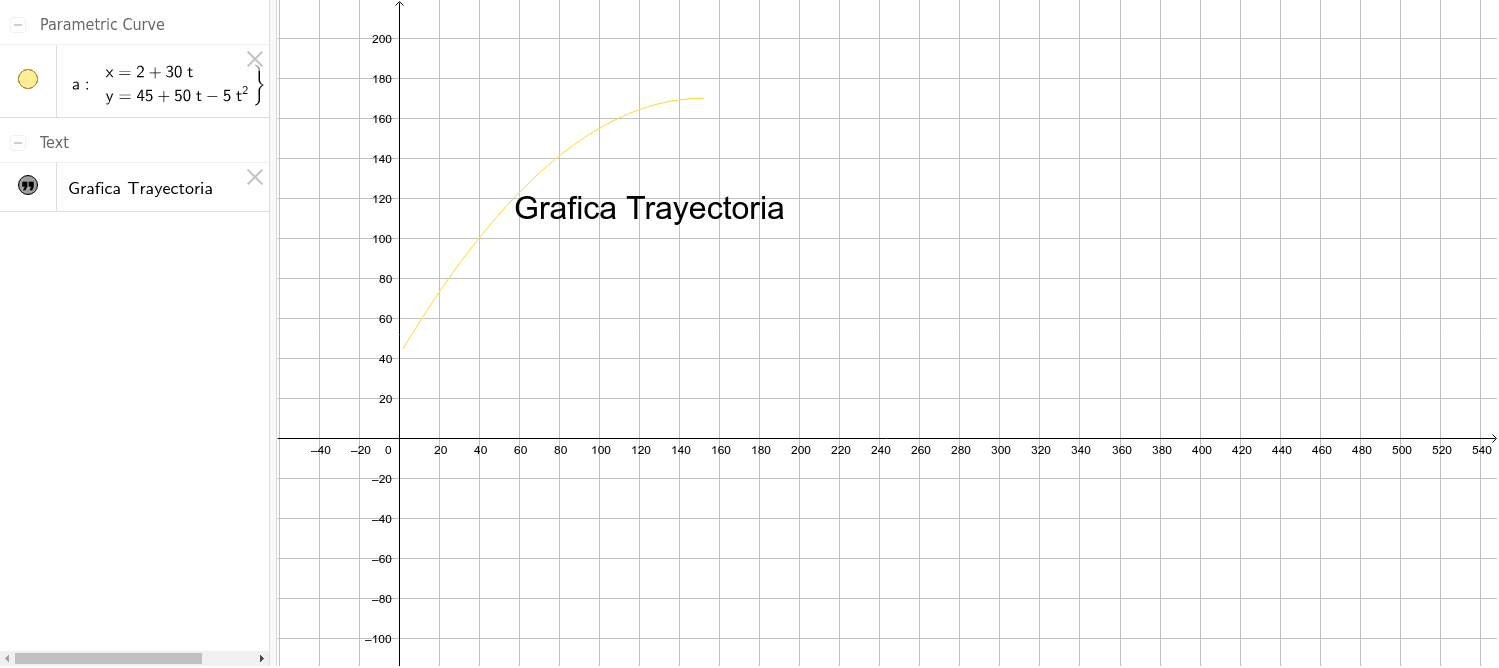
Sin embargo, cabe destacar que el logaritmo neperiano solo toma valores reales en el de, (0, +∞), ya que para valores negativos la función no está definida.
Usos y aplicaciones
El logaritmo neperiano tiene numerosas aplicaciones en diferentes áreas.
En matemáticas, se utiliza para simplificar cálculos y resolver ecuaciones exponenciales. En economía, el logaritmo neperiano se utiliza para modelar el crecimiento económico y calcular tasas de interés.
En física y estadísticas, se aplica para analizar fenómenos que siguen un crecimiento exponencial.
En resumen, la gráfica del logaritmo neperiano es una herramienta fundamental para comprender el comportamiento de esta función.
Sus características y propiedades revelan fel valiosa sobre su crecimiento y límites, y su uso se extiende a diversos campos de estudio.

Comprender la forma de esta gráfica es esencial para aprovechar al máximo las aplicaciones del logaritmo neperiano en la ciencia y las matemáticas.